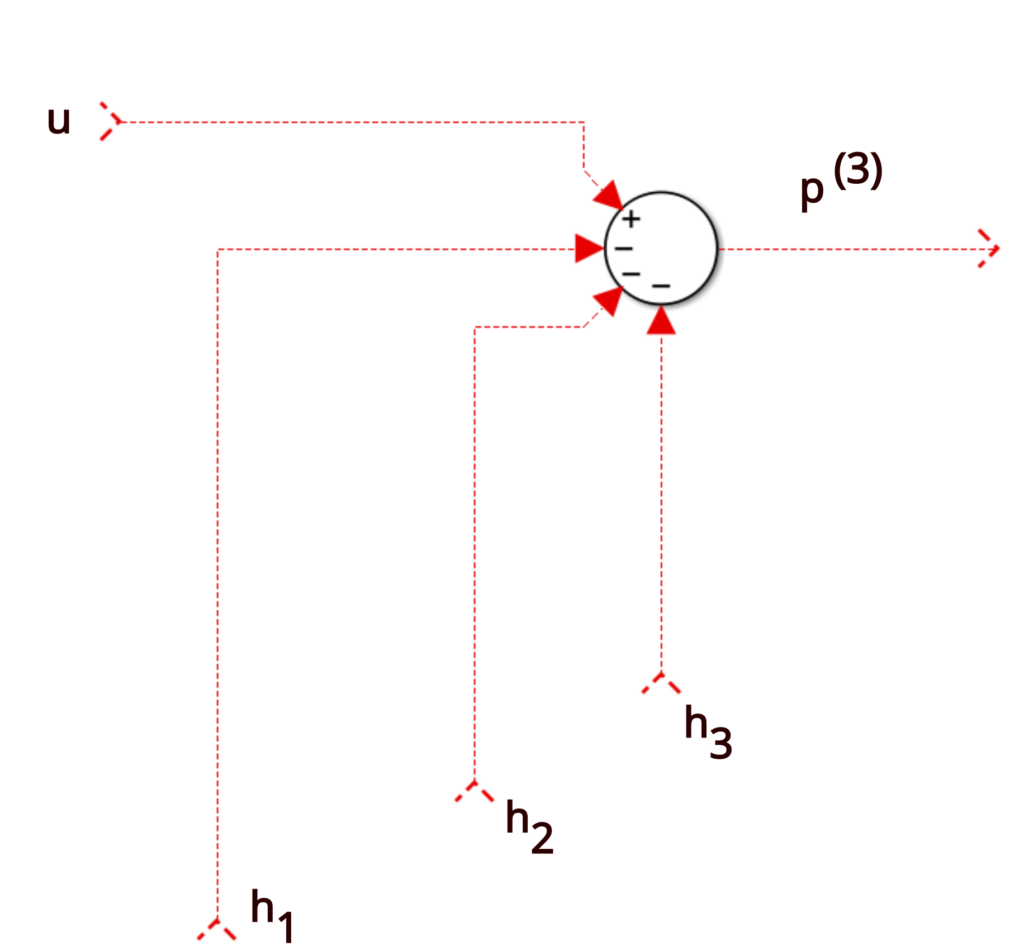
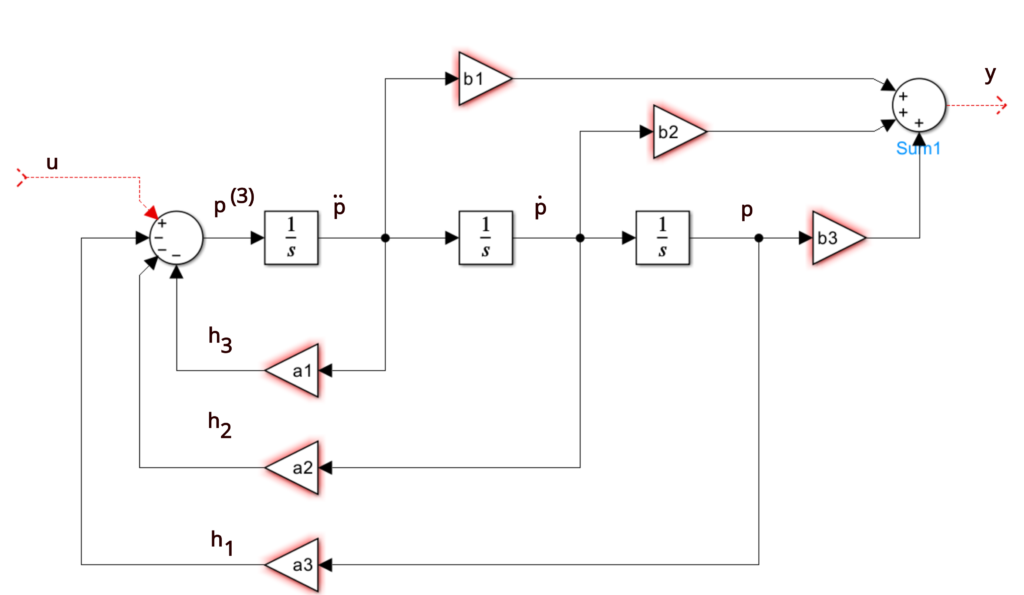
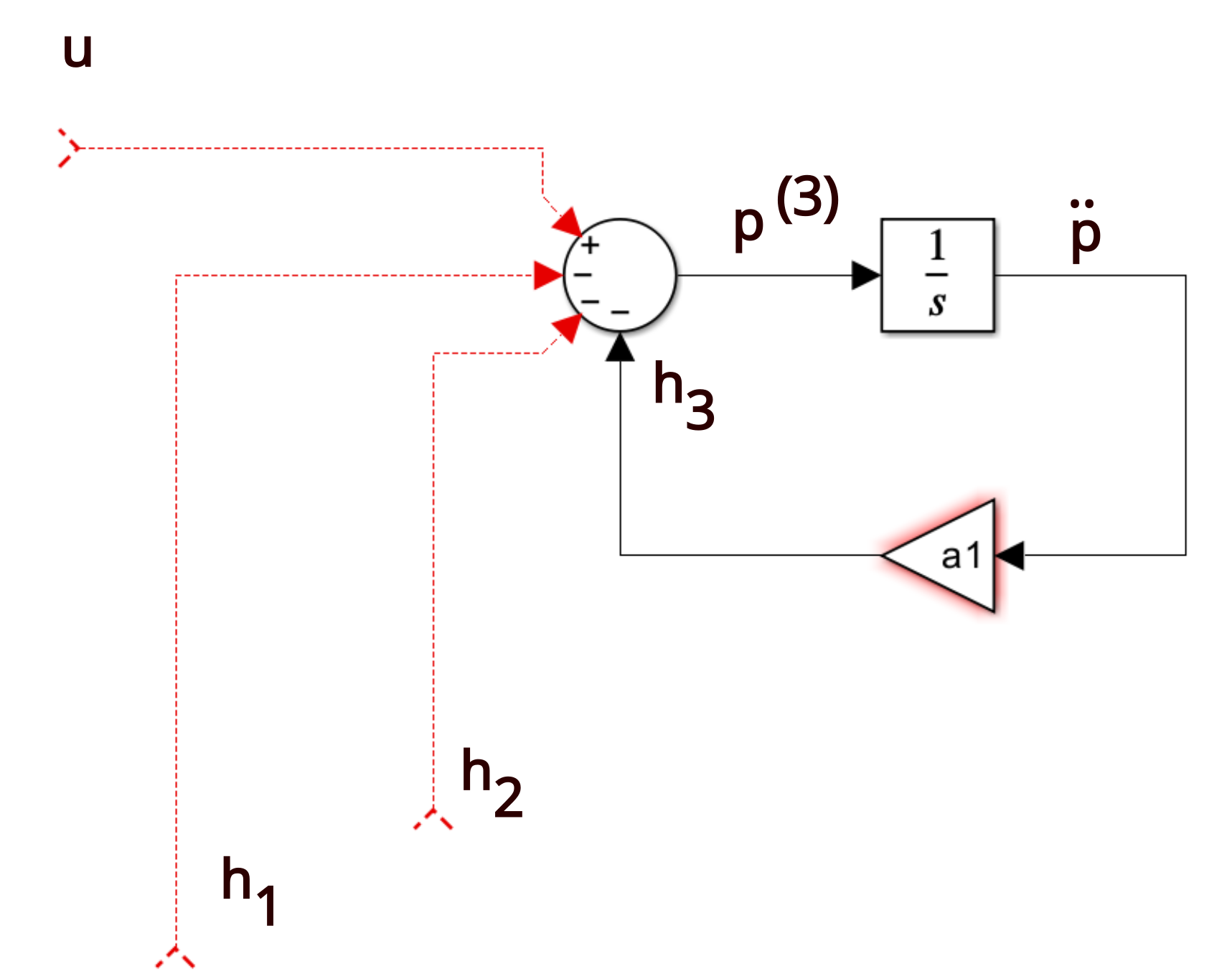
Controllable Canonical Form - Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. In this form, the characteristic polynomial of. A single transfer function has. Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. This realization is called the controllable canonical form uw linear systems (x. The observable canonical form of a system is the dual (transpose) of its controllable canonical form.
Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. A single transfer function has. In this form, the characteristic polynomial of. This realization is called the controllable canonical form uw linear systems (x. The observable canonical form of a system is the dual (transpose) of its controllable canonical form. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the.
In this form, the characteristic polynomial of. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. The observable canonical form of a system is the dual (transpose) of its controllable canonical form. A single transfer function has. This realization is called the controllable canonical form uw linear systems (x.
Control Theory Derivation of Controllable Canonical Form
Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. This realization is called the controllable canonical form uw linear systems (x. A single transfer function has. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of.
Control Theory Derivation of Controllable Canonical Form
This realization is called the controllable canonical form uw linear systems (x. In this form, the characteristic polynomial of. A single transfer function has. Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. The observable canonical form of a system is the dual (transpose) of its controllable canonical form.
Fillable Online Controllable canonical form calculator. Controllable
Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. The observable canonical form of a system is the dual (transpose) of its controllable canonical form. This realization is called the controllable canonical form uw linear systems (x. A single transfer function has. In this form, the characteristic polynomial of.
EasytoUnderstand Explanation of Controllable Canonical Form (also
A single transfer function has. In this form, the characteristic polynomial of. Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. The observable canonical form.
Solved How to derive mathematically Controllable Canonical
This realization is called the controllable canonical form uw linear systems (x. A single transfer function has. In this form, the characteristic polynomial of. The observable canonical form of a system is the dual (transpose) of its controllable canonical form. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k).
EasytoUnderstand Explanation of Controllable Canonical Form (also
In this form, the characteristic polynomial of. This realization is called the controllable canonical form uw linear systems (x. The observable canonical form of a system is the dual (transpose) of its controllable canonical form. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of.
EasytoUnderstand Explanation of Controllable Canonical Form (also
A single transfer function has. In this form, the characteristic polynomial of. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. This realization is called the controllable canonical form uw linear systems (x. The observable canonical form of a system is the dual.
Control Theory Derivation of Controllable Canonical Form
Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. In this form, the characteristic polynomial of. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. This realization is called the controllable canonical form uw.
Fillable Online Controllable canonical form calculator. Controllable
Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. In this form, the characteristic polynomial of. The observable canonical form of a system is the.
Control Theory Derivation of Controllable Canonical Form
In this form, the characteristic polynomial of. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. This realization is called the controllable canonical form uw.
Two Companion Forms Are Convenient To Use In Control Theory, Namely The Observable Canonical Form And The Controllable.
A single transfer function has. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. In this form, the characteristic polynomial of. This realization is called the controllable canonical form uw linear systems (x.